CONJUNTO DOS NÚMEROS INTEIROS
Os Números Inteiros estão presentes em nossa vida na medição de temperatura acima ou abaixo de 0 ºC.
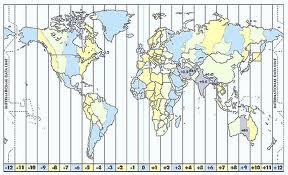
Ao situar fusos horários de países.
Identificar saldos bancários com crédito ou débito.
Contagem de gols dos times de futebol em um campeonato, entre outros.
- Apanhado histórico da origem dos sinais: Números Positivos e Negativos.
A origem e a formulação do conceito de Número ocorreu com o próprio desenvolvimento da Matemática. A partir das necessidades diárias do homem, o conceito de Número Natural surgiu naturalmente através da contagem de objetos. Assim, este conceito foi introduzido pelas nações, em conjunto com o desenvolvimento de suas formas próprias de escrita, criando o sistema de contagem.
Os números negativos apareceram pela primeira vez, no decorrer da história da Matemática, na China Antiga, aproximadamente há 4000 anos. Os chineses realizavam cálculos através de duas coleções de barras, sendo a vermelha para números positivos e a preta para números negativos. Já os matemáticos indianos descobriram os números negativos quando tentavam formular um algoritmo de resolução para equações quadráticas.
Com o início do Renascimento surgiu a expansão comercial, que aumentou a circulação de dinheiro, obrigando os comerciantes a expressarem situações envolvendo lucros e prejuízos. A maneira que eles encontraram de resolver tais situações problemas consistia no uso dos símbolos + e –. Suponha que um comerciante tenha três sacas de arroz de 10 kg cada em seu armazém. Se ele vendesse 5 Kg de arroz, escreveria o número 5 acompanhado do sinal –; se ele comprasse 7 Kg de arroz, escreveria o numeral 7 acompanhado do sinal +.
Utilizando essa nova simbologia, os Matemáticos da época desenvolveram técnicas operatórias capazes de expressar qualquer situação envolvendo números positivos e negativos. Surgia um novo conjunto numérico representado pela letra Z (significa: Zahlen: número em alemão), sendo formado pelos números positivos (Naturais) e seus respectivos opostos, podendo ser escrito da seguinte forma: Z = {...,–3, –2, –1, 0, 1, 2, 3,...}
- NÚMEROS INTEIROS.
O conjunto dos números inteiros e composto pelo conjunto dos números naturais, que receberá o nome de conjuntos dos números inteiros positivos.
Dizemos que os números naturais correspondem aos números inteiros positivos, com o zero.
E os números inteiros negativos.
Podemos representar os números inteiros de diferentes formas.
A representação abaixo é uma representação dos números inteiros em forma de conjunto.
# Note que os números naturais esta contido dentro do conjunto dos números inteiros.
(a) Conjunto dos números inteiros excluído o número zero:
Z* = {..., -4, -3, -2, -1, 1, 2, 3, 4,...}
(b) Conjunto dos números inteiros não negativos:
Z+ = {0, 1, 2, 3, 4,...}
(c) Conjunto dos números inteiros não positivos:
Z- = {..., -4, -3, -2, -1, 0}
Observação: Não existe padronização para estas notações.
- A RETA NUMÉRICA.
Uma forma de representar geometricamente o conjunto Z é construir uma reta numerada, considerar o número 0 como a origem e o número 1 em algum lugar, tomar a unidade de medida como a distância entre 0 e 1 e por os números inteiros da seguinte maneira:
Ao observar a reta numerada notamos que a ordem que os números inteiros obedecem é crescente da esquerda para a direita, razão pela qual indicamos com uma seta para a direita. Esta consideração é adotada por convenção, o que nos permite pensar que se fosse adotada outra forma, não haveria qualquer problema.
Baseando-se ainda na reta numerada podemos afirmar que todos os números inteiros possuem um e somente um antecessor e também um e somente um sucessor.
O módulo ou valor absoluto de um número Inteiro é definido como sendo o maior valor (máximo) entre um número e seu elemento oposto e pode ser denotado pelo uso de duas barras verticais | |. Assim:
|x| = max {-x,x}
Exemplos:
(a) |0| = 0
(b) |8| = 8
(c) |-6| = 6
Observação: Do ponto de vista geométrico, o módulo de um número inteiro corresponde à distância deste número até a origem (zero) na reta numérica inteira.
Dois números são opostos quando têm o mesmo módulo e sinais opostos, isto é, estão à mesma distância em relação à origem e em sentidos contrários.
|-6|= 6 Os números -6 e +6 são opostos ou simétricos.
|+6|= 6
|+2|= 2 Os números +2 e -2 também são opostos ou simétricos.
É o sinal menos que simboliza o oposto. O oposto de -2, que é +2, pode então ser escrito –(–2). Lê-se “o oposto de -2.
- COMPARAÇÃO DE NÚMEROS INTEIROS.
Conta a história que o matemático Thomas Harriot criou os símbolos > e <. Eles são usados para substituir as palavras maior que ( > ) e menor que ( < ).
+6 é menor que +12
Por símbolos representamos assim: 6 < 12
-1 é maior que -5
Por símbolos representamos assim: -1 > -5
Observações:
* Qualquer número positivo é sempre maior que qualquer número negativo.
* Na comparação de dois números positivos, o maior deles é o que está mais distantes em relação a origem zero.
* Ao comparar dois números negativos, o maior deles é aquele mais próximo em relação à origem zero.
+5 está à direita do +3. Logo, +5 > +3
-4 está à direita do -5. Logo, -4 > -5
REFERENCIA BIBLIOGRÁFICA
Guilherme Mendes, Números opostos. Disponível em http://www.professorguilherme.net/aprenda_mat/fundamental/7ano/valor%20absoluto%20ou%20modulo%20%20oposto%20%20simetricos%20%20comparacao.htm. Acessado no dia 17 de outubro de 2012.
MARCOS NOÉ, O Surgimento dos Números Inteiros. Disponível em http://www.mundoeducacao.com.br/matematica/o-surgimento-dos-numeros-inteiros.htm. Acessado no dia 15 de outubro de 2012.
Patrícia E. Silva e Ulysses Sodré, Ensino Fundamental: Números Inteiros. Disponível em http://pessoal.sercomtel.com.br/matematica/fundam/inteiros/inteiros.htm. Acessado no dia 17 de outubro de 2012.
REGINA CARLA, Matemática e educação. Disponível em http://mateeduc.blogspot.com.br/2010/04/historia-dos-numeros-inteiros.html. Acessado no dia 15 de outubro de 2012.












Nenhum comentário:
Postar um comentário